6. Intuitive Limits and Continuity
We have discussed limits as \(x\) approaches a finite number. We now turn to limits at infinity.
e. Limits at Infinity
The limit of a function \(f(x)\) as \(x\) approaches \(\infty\), denoted \(\lim\limits_{x\to\infty}f(x)\), tells what number the function approaches as \(x\) gets arbitrarily large. The precise definition of the limit at infinity is in the chapter on Precise Limits. However for most of this course, it is sufficient to understand the following intuitive definition:
A function \(f(x)\) has a limit at (positive)
infinity
if the values of the function get closer and closer to a finite
number \(L\) as \(x\) gets arbitrarily large and positive.
In that case, we say \(\lim\limits_{x\to\infty}f(x)\) exists and
is equal to \(L\), and we write:
\[
\lim\limits_{x\to\infty}f(x)=L
\]
Similarly, a function \(f(x)\) has a limit at negative
infinity
if the values of the function get closer and closer to a finite
number \(L\) as \(x\) gets arbitrarily large and negative.
In that case, we say \(\lim\limits_{x\to-\infty}f(x)\) exists and
is equal to \(L\), and we write:
\[
\lim\limits_{x\to-\infty}f(x)=L
\]
If a function has a limit \(L\), we say it is
convergent and that it
converges to \(L\).
If a function does not have a limit, we say it is
divergent or that it
diverges.
The function \(f(x)=\dfrac{2+5\cdot2^{-x}}{1+2^{-x}}\) converges to \(2\) at \(\infty\) and converges to \(5\) at \(-\infty\). Here is the plot:
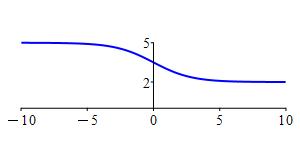
If the function diverges, it may still have an infinite limit.
If the values of a function \(f(x)\) get
arbitrarily large and positive as \(x\) gets arbitrarily
large, then we say the
function diverges to (positive) infinity
(\(+\infty\)) or that the limit is
\(+\infty\) and write:
\[
\lim\limits_{x\to\infty}f(x)=\infty
\]
If the values of a function \(f(x)\) get
arbitrarily large and negative as \(x\) gets arbitrarily
large, then we say the
function diverges to negative infinity
(\(-\infty\)) or that the limit is
\(-\infty\) and write:
\[
\lim\limits_{x\to\infty}f(x)=-\infty
\]
There are similar definitions for limits at \(-\infty\) which are
\(\pm\infty\).
If a function is divergent but does not diverge to either \(\infty\)
or \(-\infty\), then we say it is oscillatory
divergent.
We emphasize that to say the limit is positive or negative infinity does
The function \(f(x)=-5+x^2\) diverges to \(\infty\) because \(-5+x^2\) gets arbitrarily large and positive as \(x\) gets large. Its plot is:
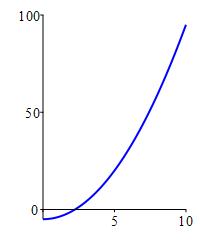
The function \(f(x)=5-x^2\) diverges to \(-\infty\) because \(5-x^2\) gets arbitrarily large and negative as \(x\) gets large. Its plot is:
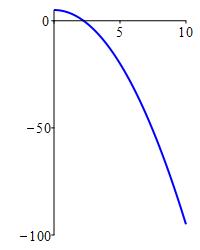
It is certainly possible to diverge without diverging to \(\infty\) or \(-\infty\).
Since the function \(f(x)=2\sin(x)\) oscillates between \(2\) and \(-2\), it does not converge; it diverges. However, it does not diverge to \(\infty\) or \(-\infty\). So it is oscillatory divergent. Its plot is:
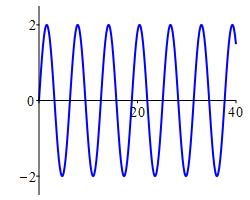
Find the limit \(\displaystyle \lim\limits_{x\to\infty}\dfrac{2x}{4+x}\).
Divide the numerator and denominator by \(x\).
\(\displaystyle \lim_{x\to\infty}\dfrac{2x}{4+x}=2\).
.jpg)
We divide the numerator and denominator by \(x\): \[ \lim\limits_{x\to\infty}\dfrac{2x}{4+x} =\lim\limits_{x\to\infty}\dfrac{2}{\dfrac{4}{x}+1} \] As \(x\) gets large, \(\dfrac{1}{x}\) approaches \(0\). So: \[ \lim\limits_{x\to\infty}\dfrac{2x}{4+x} =\dfrac{2}{0+1}=2 \]
.jpg)
Techniques for computing limits appear in the next chapter.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum